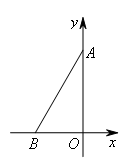
如图，在平面直角坐标系中，点A，B分别在y轴和x轴上，∠ABO=60°，在坐标轴上找一点P，使得△PAB是等腰三角形，则符合条件的点P共(    )个．

要使△PAB是等腰三角形，而AB为定线段，
所以要考虑AB作为等腰三角形的腰还是底，
①当AB作为等腰三角形的腰时，
分别以点A，B为圆心，AB长为半径画圆，
此时，圆与坐标轴的交点个数为8个，
排除与A，B重合的点以及两个圆的一个交点，
故满足条件的点P的个数为5个；
②当AB作为等腰三角形的底时，
作线段AB的垂直平分线，此时与坐标轴有2个交点，
排除与两圆的交点，故满足条件的点P的个数为1个；
因此满足条件的P点共有6个．
故选C

略