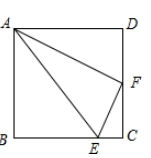
在正方形ABCD中，F是CD的中点，E在BC上，且BE：CE=3:1，则∠AFE=(    )

解：∵BE：CE=3:1，
设BE=3a，则CE=a，
正方形ABCD的边长为4a，
∵F是CD的中点，
∴DF=CF=2a
在Rt△ADF中，由勾股定理得AF²=20a²，
同理，EF²=5a²，AE²=25a²，
∴EF²+ AF²=AE²
由勾股定理逆定理得，△AEF为直角三角形，且∠AFE=90°
故选C

略