如图，点E是等边三角形ABC内一点，且EA=EB，△ABC外一点D满足BD=AC，且BE平分∠DBC，则∠BDE等于(    )

要求∠BDE的度数，缺少条件，考虑转化，连接CE，
可证△DBE≌△CBE（SAS），求∠BDE就转化为求∠3．
猜测∠3=∠4，需通过证明△ACE≌△BCE得到．
如图，连接CE．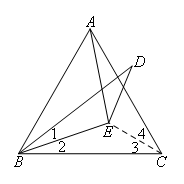

∵△ABC是等边三角形，
∴AC=BC=AC，∠ACB=60°，
∵BE平分∠DBC，
∴∠1=∠2．
∵BD=AC，
∴BD=BC，
又∵BE=BE，
∴△DBE≌△CBE（SAS），
∴∠BDE=∠3．
∵EA=EB，AC=BC，CE=CE，
∴△ACE≌△BCE（SSS），
∴∠3=∠4，
∴∠3=30°，
∴∠BDE=30°．
故选B．

略