如图,点P是∠BAC的平分线AD上一点,且∠BAC=30°,PE∥AB交AC于点E,已知AE=2,则点P到AB的距离是( )
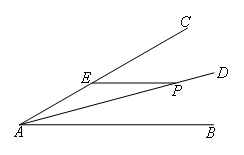
- A.1
- B.1.5
- C.2
- D.3
答案
正确答案:A
知识点:含30°角的直角三角形 角平分线加平行会出现等腰三角形
如图,过P作PF⊥AC于F,PM⊥AB于M,
PM的长即为点P到AB的距离.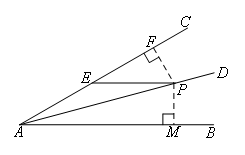
∵AD是∠BAC的平分线,PF⊥AC,PM⊥AB,
∴PF=PM,∠EAP=∠PAM,
∵PE∥AB,
∴∠EPA=∠PAM,
∴∠EAP=∠EPA,
∴AE=PE
∵AE=2,
∴PE=2,
∵∠BAC=30°,PE∥AB,
∴∠FEP=∠BAC=30°,
在Rt△PEF中,∠PEF=30°,
∴![]() ,
,
∴PM=1.
故选A.
略








