如图,在△ABC中,AB=AC,AD平分∠BAC,D,E是△ABC内两点,且∠ECB=∠E=60°,若CE=8,DE=2,则CD=( )

- A.
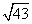
- B.10
- C.

- D.
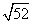
答案
正确答案:C
知识点:略
如图,延长AD交BC于点F,延长ED交BC于点H,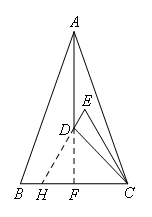
∵∠ECB=∠E=60°
∴△CEH是等边三角形
∵CE=8,DE=2
∴DH=6,CH=8
∵在△ABC中,AB=AC
∴△ABC是等腰三角形
∵AD平分∠BAC
∴AD是三线合一的线
∴AD⊥BC
在Rt△DFH中,∠DHF=60°,DH=6
∴HF=3,DF=![]()
∴CF=CH-HF=8-3=5
在Rt△CDF中,![]()
故选C
略








