如图1，直线AM∥BN，∠MAB与∠NBA的平分线交于点C，过点C作一条直线与两条直线MA，NB分别相交于点D，E．
（1）如图1所示，当直线与直线MA垂直时，求证：AB=AD+BE．

下面给出了证明的路线图，如图：

请你仔细观察下列序号所代表的内容：
①∠CEB=90°，∠1=∠3；②AB=BF；③AC=CF；④AB=BF，AD=EF；⑤△ACB≌△FCB（SAS）；⑥△ADC≌△FEC（ASA）．
以上横线处，依次所填最恰当的是(    )

• A.②③⑥
• B.①④⑤
• C.②③⑤
• D.①④⑥

答案

正确答案：A

知识点：略  

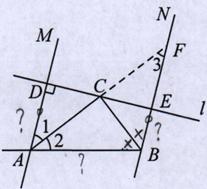
要证AB=AD+BE，考虑把AD和BE转到同一条直线上，
延长AC交BN于点F，只要证明AB=BF，AD=EF即可．
由平行和角平分线可以证得∠2=∠3，因此AB=BF，
结合BC平分∠ABF，由等腰三角形三线合一可以证得AC=CF，
进而可以证得△ADC≌△FEC（ASA），通过转移边可以证得AB=AD+BE．
因此，横线处依次所填最恰当的是②③⑥．
故选A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题