如图,在四边形ABCD中,AD∥BC,AB=AD+BC,M是CD的中点,若∠ABC=50°,则∠BAM=( )
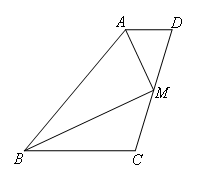
- A.75°
- B.65°
- C.25°
- D.50°
答案
正确答案:B
知识点:略
如图,延长AM交BC的延长线于点E.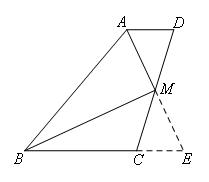
∵AD∥BC,
∴∠D=∠MCE,∠DAM=∠E,
∵M是CD的中点,
∴DM=CM,
∴△ADM≌△ECM(AAS),
∴AD=EC,AM=EM,
∴BE=BC+CE=BC+AD=AB,
∴△ABE是等腰三角形,
∵∠ABC=50°,
∴∠BAM=∠E=65°.
故选B
略








