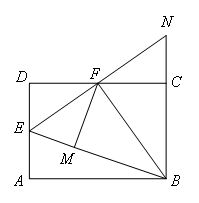
如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F，将△DEF沿EF折叠，点D恰好落在BE上点M处，延长BC，EF交于点N．有下列四个结论：①DF=CF；②BF⊥EN；③△BEN是等边三角形；④S_△BEF=3S_△DEF．其中正确结论的序号是(    )

①正确，理由：
由△BMF≌△BCF（∠FBM=∠FBC，∠FCB=∠FMB，BF=BF），
可得MF=CF，
由折叠可得，DF=MF，
∴DF=CF
②正确，理由：
由△BMF≌△BCF可得∠CFB=∠MFB，
由折叠可得，∠DFE=∠MFE，
又∵∠CFB+∠MFB+∠DFE+∠MFE=180°，
∴∠EFB=90°，BF⊥EN
③错误，理由：
假如△BEN为等边三角形，
则∠ABE=∠EBF=∠FBN=30°，可得BE=2AE，
而BE=BM+ME=BC+ME=2AE+AE=3AE，与BE=2AE矛盾，
∴△BEN不是等边三角形
④正确，理由：
∵BE=3EM，
∴S_△BEF=3S_△MEF=3S_△DEF．
故选B

略