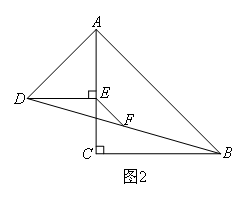
（上接第1题）将图1中的△AED绕点A顺时针旋转，使△AED的一边AE恰好与△ACB的边AC在同一条直线上（如图2），连接BD，取BD的中点F，延长EF交BC于点M，连接CF即可得到CE与FE之间的数量关系，则此思路得到线段CE与FE之间的数量关系的依据是(    )

（思路：类比上一题，只需证明△CEF是等腰直角三角形即可.但此时“直角+中点”的特征发生变化，观察图形，选用“平行+中点”）
如图，延长EF，交BC于点M，连接CF.

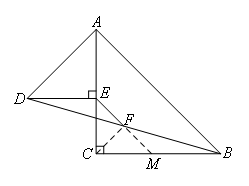
∵∠DEC=∠ACB=90°，
∴DE∥BC，
∴∠EDF=∠MBF.
又∵DF=BF，∠EFD=∠MFB，
∴△DEF≌△BMF（ASA），
∴DE=BM.
∵DE=AE，
∴CE=CM，
∴△CEM是等腰直角三角形，
∴CF⊥ME（等腰三角形三线合一），
∠CEF=45°，
∴△CEF是等腰直角三角形，
∴（等腰直角三角形三边关系）.
综上，得到结论需要用到等腰三角形三线合一、等腰直角三角形三边关系.
故选D

略