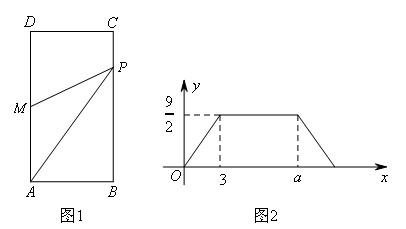
如图1,长方形ABCD中,AB=3,M是AD的中点,点P在长方形的边上,从点A出发,沿A→B→C→D运动,到达点D运动停止.设点P经过的路程为x,△APM的面积为y,y与x的关系图象如图2所示,则BC的长和a的值分别为( )
- A.BC=6,a=9
- B.BC=9,a=6
- C.BC=
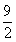 ,a=9
,a=9 - D.BC=6,a=12
答案
正确答案:A
知识点:略
关系图象上横轴表示点P经过的路程,纵轴表示△APM的面积,
当P在AB上运动时,△AMP的面积,底AM不变,高AP逐渐增大,
即面积不断增大;
当P在BC上运动时,△AMP的面积,底AM不变,高等于AB不变,
即面积不变;
当P在CD上运动时,△AMP的面积,底AM不变,高DP逐渐减小,
即面积不断减小;
所以点B和点C为点P运动过程中的状态转折点,
当x=3时,y=![]() ,此时对应的即为转折点B.所以AB=3,
,此时对应的即为转折点B.所以AB=3,![]() ×AM×AB=
×AM×AB=![]() ,可知AM=3,
,可知AM=3,
因为M是AD的中点,所以BC=AD=2AM=6.
因为P在BC上运动时,△AMP的面积不变,所以BC=a-3,可得a=9.
故选A.
略








