如图,在Rt△ABC中,∠ACB=90°,BC=2,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5,则AE=( )
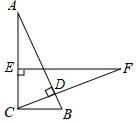
- A.5
- B.4
- C.3
- D.2
答案
正确答案:C
∵CD⊥AB,EF⊥AC
∴∠ADC=∠FEC=90°
∴∠A+∠ACD=90°,∠F+∠ACD=90°
∴∠A=∠F
在△ABC和△FCE中,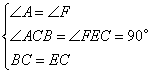
∴△ABC≌△FCE(AAS)
∴AC=EF=5
∵EC=BC=2
∴AE=AC-EC=3
故选C.
略




正确答案:C
∵CD⊥AB,EF⊥AC
∴∠ADC=∠FEC=90°
∴∠A+∠ACD=90°,∠F+∠ACD=90°
∴∠A=∠F
在△ABC和△FCE中,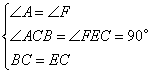
∴△ABC≌△FCE(AAS)
∴AC=EF=5
∵EC=BC=2
∴AE=AC-EC=3
故选C.
略
