已知:如图,在四边形ABCD中,AD∥BC,E为AB的中点,G,F分别为AD,BC边上的点,且GE⊥EF.
求证:GF=AG+BF.
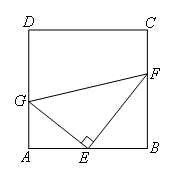
如图,先在图上走通思路后再填写空格内容:

①因为AD∥BC,E为AB的中点,考虑延长GE交FB的延长线于点H;
②进而利用全等三角形的判定 ,证明 ≌ ;
③由全等可得 ;
④结合已知条件,得EF垂直平分GH,根据线段垂直平分线上的点到这条线段两个端点的距离相等,可得 ,可得FG=AG+BF.
以上空缺处依次所填最恰当的是( )
- A.②AAS或ASA,△AEG,△BEH;③AG=BH,∠A=∠EBH;④FG=FH
- B.②SAS,△AEG,△BEH;③AG=BH,∠A=∠EBH;④FG=FH
- C.②AAS或ASA,△AEG,△BEH;③AG=BH,EG=EH;④FG=FH
- D.②ASA,△AEG,△BEH;③AG=BH;④FG=FH
答案
正确答案:C
知识点:三角形全等之倍长中线
要证明GF=AG+BF,这三条线段比较分散,
考虑作辅助线将它们集中,AD∥BC,E为AB边的中点,
这是平行夹中点结构,利用倍长的思想,
如图,延长GE交FB的延长线于点H.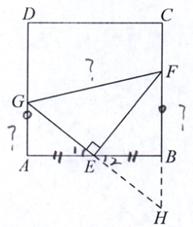
∵AD∥BC
∴∠AGE=∠H
∵E为AB的中点
∴AE=BE
在△AEG和△BEH中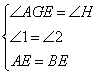
∴△AEG≌△BEH(AAS)
∴AG=BH,EG=EH
∵GE⊥EF
∴∠FEG=∠FEH
在△FEG和△FEH中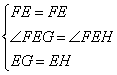
∴△FEG≌△FEH(SAS)
∴FG=FH
∵FH=FB+BH
∴FG=FB+AG
即GF=AG+BF.
(其中,证明全等时也可以先由AD∥BC得∠A=∠EBH,
再结合AE=BE,∠1=∠2,利用ASA证明△AEG≌△BEH.)
故选C.
略









