已知：如图，在四边形ABCD中，AB=AD，E，F分别是DC，BC上的点，且满足
，∠D+∠ABC=180°．
求证：EF=BF+DE．
先在图上走通思路后再填写空格内容：
①要证明EF=BF+DE，是线段的和差倍分，考虑 ，解决本题用的是 ；
②结合条件∠D+∠ABC=180°，考虑 （辅助线），然后证全等，理由是 ；
③由已证的全等和条件，得 ，然后证全等，理由是 ，由全等的性质得 ，从而得EF=BF+DE．
以上空缺处依次所填最恰当的是( )
- A.①截长补短；补短②延长CB到G，使BG=DE，连接AG；SAS③∠G=∠AEF；SSA；GF=EF
- B.①截长补短；截长②在FE上截取FG，使FG=BF，连接AG；SAS③∠GAE=∠DAE；SAS；GE=DE
- C.①截长补短；补短②延长CB到G，使BG=DE，连接AG；SAS③∠GAF=∠EAF；SAS；GF=EF
- D.①截长补短；截长②在EF上截取EG，使EG=ED，连接AG；SAS③∠GAF=∠BAF；SAS；GF=BF
答案
正确答案：C
知识点：三角形全等之截长补短
看到线段的和差倍分，考虑截长补短，这里采用补短．
条件中有∠D+∠ABC=180°，因此考虑延长CB到G，使BG=DE，
连接AG，可以得到∠ABG=∠D，只需要证明EF=GF即可．
结合已知条件，利用SAS可以证明△ABG≌△ADE，进而得到AG=AE，
∠DAE=∠BAG，结合
可以得到∠GAF=∠EAF，
进而证明△GAF≌△EAF（SAS），得到GF=EF．
证明：如图，延长CB到G，使BG=DE，连接AG．
∵∠D+∠ABC=180°
∠1+∠ABC=180°
∴∠1=∠D
在△ABG和△ADE中
∴△ABG≌△ADE（SAS）
∴AG=AE，∠4=∠3
∵
∴∠2+∠3=∠EAF
∴∠2+∠4=∠EAF
即∠GAF=∠EAF
在△GAF和△EAF中
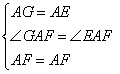
∴△GAF≌△EAF（SAS）
∴GF=EF
∵GF=BF+BG
=BF+DE
∴EF=BF+DE
故选C．
略
WORD格式（