已知点O是△ABC内任意一点，连接OA并延长到点E，使得AE=OA，以OB，OC为邻边作□OBFC，连接OF，与BC交于点H，连接EF．
（1）问题发现：如图1，若△ABC为等边三角形，线段EF与BC的位置关系是        ，数量关系为          ．(    )

• A.EF⊥BC；EF=BC
• B.EF⊥BC；EF=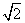BC
• C.EF⊥BC；EF=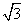BC
• D.EF⊥BC；EF=2BC

答案

正确答案：C

知识点：略  

如图，连接AH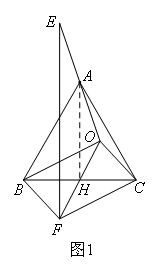

∵四边形OBFC是平行四边形，对角线OF、BC交于点H
∴OH=FH，BH=CH
∴AH为△OEF的中位线
∴AH∥EF且AH=EF
∵△ABC是等边三角形，点H为BC的中点
∴AH⊥BC，且AH=BC
∴EF⊥BC，且EF=2AH=
故选C

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题