已知等腰三角形ABC中，∠ACB=90°，点E在AC的延长线上，且∠DEC=45°，M，N分别是DE，AE的中点，连接MN，交直线BE于点F．
（1）如图1，当点D在CB的延长线上时，线段MF，FN，BE之间的数量关系为( )
- A.
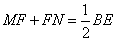
- B.
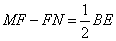
- C.
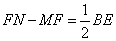
- D.
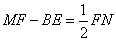
答案
正确答案：A
知识点：略
如图，连接AD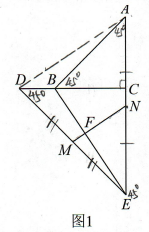
∵M，N分别是DE，AE的中点
∴MN为△ADE的中位线
∴MN=
AD，即MF+FN=AD
∵∠ACB=90°，点E在AC的延长线上，且∠DEC=45°
∴△ABC是等腰直角三角形∠DCE=90°
∴△DCE是等腰直角三角形
可证△ADC≌△BEC
∴AD=BE
∴MF+FN=BE
故选A
略
WORD格式（