如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AB=OB,点E,点F分别是OA,OD的中点,连接EF,∠CEF=45°,EM⊥BC于点M,EM交BD于点N,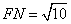 ,则线段BC的长为( )
,则线段BC的长为( )
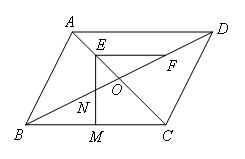
- A.
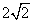
- B.
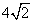
- C.
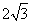
- D.
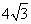
答案
正确答案:B
知识点:略
如图,连接BE
在平行四边形ABCD中,BC∥AD,BC=AD,
∵点E,F分别是OA,OD的中点
∴EF=![]() AD=
AD=![]() BC,EF∥AD∥BC,∠ECB=∠CEF=45°
BC,EF∥AD∥BC,∠ECB=∠CEF=45°
∵△AOB是等腰三角形且点E为AO的中点
∴BE⊥AC,∠BEC=90°
∴△BEC是等腰直角三角形
∵EM⊥BC
∴EM=BM=CM
∴EF=BM
∴△BNM≌△FNE
∴NB=![]() ,EN=MN
,EN=MN
设EN=MN=x,则BM=EM=2x
根据勾股定理,![]()
解得x=![]()
∴BM=2![]() ,BC=2BM=4
,BC=2BM=4![]()
所以则线段BC的长为4![]()
故选B
略








