已知：在平面直角坐标系中，A（0，1），B（2，0），C（-2，0）．设点P在坐标轴上（不与C重合），且△ABP与△ABC的面积相等，求点P的坐标为(    )

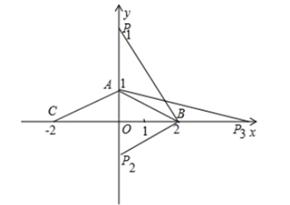
∵A（0，1），B（2，0），C（-2，0）
∴BC=4，OA=1
∴
①当点P在y轴上时，
则有
∵OB=2
∴AP=2
∴当P位于A上边时，P（0，3）
当P位于A下边时，P（0，-1）
②当点P在x轴上时，
则有
∵OA=1
∴BP=4
∴当P位于B右边时，P（6，0）
当P位于B左边时，P（-2，0），与C重合，舍去
综上，点P坐标为（0，3），（0，-1），（6，0）
故选D．

略