正方形ABCD在平面直角坐标系中的位置如图所示，已知A点坐标为(0，a)，B点坐标为(b，0)，则C点的坐标为(    )

如图，过点C作CE⊥x轴于点E，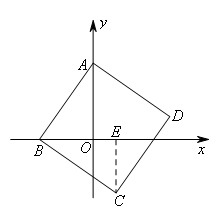

∵A点坐标为(0，a)，B点坐标为(b，0)，
∴OA=a，OB=-b，
∵四边形ABCD为正方形，
∴AB=BC，∠ABC=90°，
∴∠ABO+∠CBE=90°，
又∠ABO+∠BAO=90°，
∴∠BAO=∠CBE，
在△ABO和△BCE中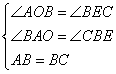

∴△ABO≌△BCE（AAS）
∴CE=OB=-b，BE=OA=a，
∴OE=BE-OB=a+b，
∵点C在第四象限，
∴点C的坐标为(a+b，b)
故选C

略