已知：在Rt△ABC中，∠C=90°，BC=4，AC=8，点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为E、F，得四边形DECF，设DE=x，DF=y；
(1)用含y的代数式表示AE；
(2)求y与x之间的函数关系式，并求出x的取值范围；
(3)设四边形DECF的面积为S，求出S的最大值.
答案
(1) AE=8-y；
(2)y=8-2x(0＜x＜4)；
(3) S的最大值8．
如图：
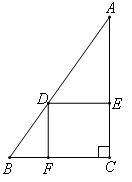
（1）由已知得DECF是矩形，故EC=DF=y，AE=8-EC=8-y；
（2）∵DE∥BC，∴△ADE∽△ABC，根据相似三角形的对应边对应成比例得：＝
，即
＝
，所以y＝8－2x（0＜x＜4）.
（3）S=xy=x（8-2x）=-2（x-2）2+8，∴当x=2时，S有最大值8．
对二次函数的相关知识不是很了解，不会运用二次函数的性质求最值的问题
WORD格式（
