如图，在△ABC中，AO平分∠BAC，BO平分∠ABC，作OD⊥AB于点D，连接CO．
（1）求证：CO平分∠ACB；
（2）当AB=7，BC=8，AC=9时，AD的长为        ．（请直接写出答案）

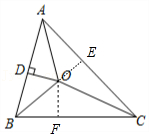
（1）证明：过O点作OE⊥AC于E，OF⊥BC于F，如图，
∵AO平分∠BAC，OD⊥AB，OE⊥AC，
∴OD=OE，
∵BO平分∠ABC，OD⊥AB，OF⊥BC，
∴OD=OF，
∴OE=OF，
∴CO平分∠ACB；
（2）解：设AD=x，则BD=AB﹣AD=7﹣x，
在Rt△AOD和Rt△AOE中，
，
∴Rt△AOD≌Rt△AOE（HL），
∴AD=AE=x，
∴CE=AC﹣AE=9﹣x，
同理可证明Rt△BOD≌Rt△BOF，Rt△COE≌Rt△COF，
∴BD=BF=7﹣x，CE=CF=9﹣x，
∵BC=8，
∴7﹣x+9﹣x=8，解得x=4，
即AD的长为4．

略