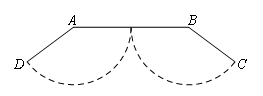
如图，标记门槛两端点为A，B，门缝下端点为C，D，推开两扇门，测量得到点C，D到门槛AB所在直线的距离都是6，C，D两点之间的距离为36，则AB的长为(    )

解：OA=OB=AD=BC，过点C作CE⊥AB于E，则CE=6；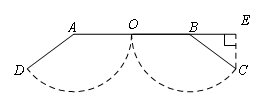

∵C，D两点之间的距离为36
∴OE=18
设OB=BC=x，
则BE=18-x
在Rt△BCE中，由勾股定理得：
(18-x)²+6²=x²解得x=8，
则AB=2OB=2×(18-8)=20
故选：D

略