(1)特例发现:如图1,AB∥CD,CE平分∠ACD,AE平分∠BAC.请观察猜想∠AEC的度数并说明理由;
(2)类比探究:如图2,点M是AE上一点,当∠E=90°保持不变,移动直角顶点E,使CE平分∠MCD.
∠BAE与∠MCD存在怎样的数量关系?并说明理由;
(3)拓展应用:如图3,P为线段AC上一定点,点Q为直线CD上一动点,点Q不与点C重合.
∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.
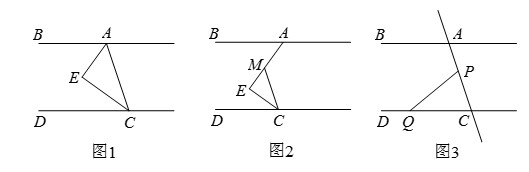
答案
(1)∠AEC=90°;
(2)∠BAE+![]() ∠MCD=90°;
∠MCD=90°;
(3)∠BAC=∠PQC+∠QPC或∠PQC+∠QPC+∠BAC=180°.
知识点:平行线的性质
证明:(1)∠AEC=90°,理由如下:
如图1,
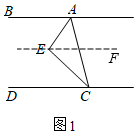
过点E作EF∥AB,则∠BAE=∠AEF,
因为AB∥CD,
所以EF∥AB,且∠BAC+∠ACD=180°,
所以∠DCE=∠FEC,
因为CE平分∠ACD,AE平分∠BAC,
所以∠BAC=2∠EAC,∠ACD=2∠ACE,
因为∠BAC+∠ACD=180°,
所以∠EAE+∠DCE=90°,
即∠AEC=90°;
(2)![]() ,理由:
,理由:
如图2,过E作EF∥AB,
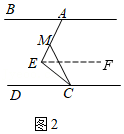
因为AB∥CD,
所以EF∥AB∥CD,
所以∠BAE=∠AEF,∠FEC=∠DCE,
因为∠E=90°,
所以∠BAE+∠ECD=90°,
因为CE平分∠MCD,
所以∠MCE=∠ECD![]() ∠MCD,
∠MCD,
所以∠BAE![]() MCD=90°;
MCD=90°;
(3)如图3,当点Q在射线CD上运动时,∠BAC=∠PQC+∠QPC,
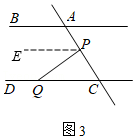
理由:过点过P作PE∥AB,
因为AB∥CD,
所以EF∥AB∥CD,
所以∠BAC=∠EPC,∠PQC=∠EPQ,
所以∠BAC=∠PQC+∠QPC;
如图4,当点Q在射线CD的反向延长线上运动时(点C除外)∠PQC+∠QPC+∠BAC=180°,
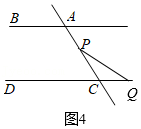
理由:因为AB∥CD,
所以∠BAC=∠ACQ,
因为∠PQC+∠PCQ+∠ACQ=180°,
所以∠PQC+∠QPC+∠BAC=180°,
综上,∠BAC=∠PQC+∠QPC或∠PQC+∠QPC+∠BAC=180°.
略








