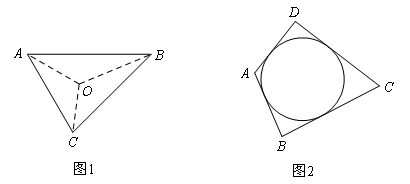
阅读材料：如图1，△ABC的周长为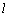，内切圆O的半径为r，连接OA，OB，OC，△ABC被划分为三个小三角形，用S_△ABC表示△ABC的面积．
∵S_△ABC=S_△OAB+S_△OBC+S_△OCA
又∵S_△OAB=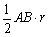，S_△OBC=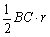，S_△OCA=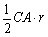
∴S_△ABC=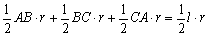
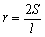∴（可作为三角形内切圆半径公式）
根据上述阅读材料完成下列各题：
（1）理解与应用：利用公式计算边长分别为5，12，13的三角形内切圆的半径；
（2）类比与推理：若四边形ABCD存在内切圆（与各边都相切的圆，如图2）且面积为S，各边长分别为a，b，c，d，试推导四边形的内切圆半径公式；
（3）拓展与延伸：若一个n边形（n为不小于3的整数）存在内切圆，且面积为S，各边长分别为a₁，a₂，a₃，…，a_n，合理猜想其内切圆半径公式（不需说明理由）．

答案

（1）内切圆半径为2；
（2）；
（3）．

知识点：三角形的内切圆  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>