已知数轴上有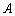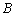，两点，分别代表-40，20，两只电子蚂蚁甲、乙分别从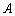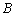，两点同时出发，甲沿线段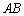以1个单位长度/秒的速度向右运动，甲到达点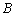处时运动停止，乙沿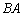方向以4个单位长度/秒的速度向左运动．
（1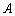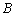），两点间的距离为      个单位长度；乙到达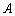点时共运动了      秒．
（2）甲、乙在数轴上的哪个点相遇？
（3）多少秒时，甲、乙相距10个单位长度？
（4）若乙到达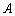点后立刻掉头并保持速度不变，则甲到达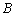点前，甲、乙还能在数轴上相遇吗？若能，求出相遇点所对应的数；若不能，请说明理由．

（1）A，B两点的距离为AB＝|﹣40﹣20|＝60；
秒
（2）设它们按上述方式运动，甲，乙经过x秒会相遇
x+4x=60，
解得x=12秒，
-40+12=-28．
（3）两种情况，相遇前，
设y秒时，甲、乙相距28个单位长度，y+4y＝60﹣10，
解得：y＝10，
第一次相遇后，
设y秒时，甲、乙相距10个单位长度，
y+4y﹣60＝10，
解得：y＝14，
综上，10秒或14秒时，甲、乙相距10个单位长度；
（4）甲到达B点前，甲，乙不能在数轴上相遇，
理由：设甲到达B点前，甲，乙经过a秒在数轴上相遇，
根据题意得，a＝4a-60，
解得：a＝20，
2a＝1×20＝2060，
故甲，乙能在数轴上相遇．相遇的点为-40+20=-20

略