探究发现
（1）如图1，在△ABC中，点P是内角∠ABC和外角∠ACD的角平分线的交点，试猜想∠P与∠A之间的数量关系，并证明你的猜想．
迁移拓展
（2）如图2，在△ABC中，点P是内角∠ABC和外角∠ACD的n等分线的交点，即∠PBC=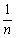∠ABC，∠PCD=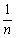∠ACD，试猜想∠P与∠A之间的数量关系，并证明你的猜想．
应用创新
（3）如图3，已知AD，BE相交于点C，∠ABC，∠CDE，∠ACE的平分线交于点P，若∠A=35°，∠E=25°，则∠BPD=        ．

答案

（1）∠P=∠A；
（2）∠P=∠A；
（3）30°．

知识点：角平分线  三角形内角和  外角  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>