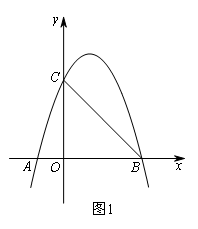
（2020眉山）如图1，抛物线y=-x²+bx+c与x轴交于A，B两点，与y轴交于点C，已知点B坐标为(3，0)，点C坐标为(0，3)．
（1）求抛物线的表达式．
（2）点P为直线BC上方抛物线上的一个动点，当△PBC的面积最大时，求点P的坐标．
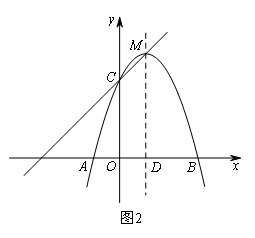
（3）如图2，点M为该抛物线的顶点，直线MD⊥x轴于点D，在直线MD上是否存在点N，使点N到直线MC的距离等于点N到点A的距离？若存在，求出点N的坐标；若不存在，请说明理由．

答案

（1）y=-x²+2x+3；
（2）P(，)；
（3）存在，点N的坐标为(1，)或(1，)．

知识点：存在性问题  二次函数的图象与性质  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>