将全等的Rt△ABC和Rt△DBE按图1方式摆放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，点E落在AB上，DE所在直线交AC所在直线于点F．
（1）求证：AF+EF=DE．
（2）若将图1中的△DBE绕点B按顺时针方向旋转角α，且0°<α<60°，其他条件不变，请在图2中画出变换后的图形，并直接写出（1）中的结论是否仍然成立．
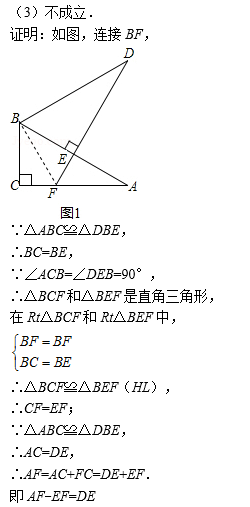
（3）若将图1中的△DBE绕点B按顺时针方向旋转角β，且60°<β<180°，其他条件不变，如图3．你认为（1）中的结论还成立吗？若成立，写出证明过程；若不成立，请写出此时AF，EF与DE之间的关系，并说明理由．

答案

（1）证明略；
（2）成立；
（3）不成立，AF-EF=DE．

知识点：全等三角形的判定和性质  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>