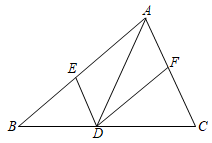
如图，在△ABC中，点D，E，F分别在边AB，BC，CA上，且DE∥CA，DF∥BA，下列四种说法：
①四边形AEDF是平行四边形；
②如果∠BAC=90°，那么四边形AEDF是菱形；
③如果AD平分∠BAC，那么四边形AEDF是菱形；
④如果AB=AC，那么四边形AEDF是菱形．
其中，正确的有(    )

• A.①②③
• B.①③④
• C.①③
• D.③④

答案

正确答案：C

知识点：菱形的判定  

∵DE∥CA，DF∥BA，∴四边形AEDF是平行四边形，故①正确；
∵∠BAC=90°，四边形AEDF是平行四边形，
∴四边形AEDF是矩形，故②错误；
∵AD平分∠BAC，四边形AEDF是平行四边形，
∴四边形AEDF是菱形，故③正确；
∵AB=AC，四边形AEDF是平行四边形，
不能得出AE=AF，故四边形AEDF不一定是菱形，故④错误；
故选C

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>