如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,E为MN的中点,连接AE,则线段AE的最小值为( )
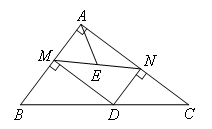
- A.
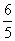
- B.
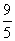
- C.
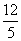
- D.3
答案
正确答案:A
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=90°,
又∵∠BAC=90°,
∴四边形ANDM为矩形,
∵E为对角线MN的中点,
∴![]() ,
,
∴当AD最小时,线段AE有最小值.
如图,过点A作AD⊥BC于点D,此时AD取得最小值,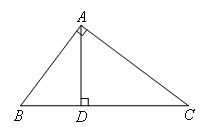
在Rt△ABC中,∠BAC=90°,BA=3,AC=4,
由勾股定理得,BC=5,
∴![]() ,
,
∵AD⊥BC,
∴![]()
∴![]() ,
,
∴![]() .
.
略





