证明：（1）重心定理：三角形顶点到重心的距离等于该顶点对边上中线长的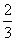．（注：重心是三角形三条中线的交点）
（2）角平分线定理：三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例．

答案

证明：（1）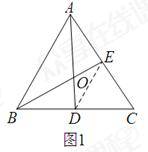
如图1，AD、BE为△ABC的中线，且AD、BE交于点O连接DE
∵AD、BE是△ABC的中线
∴DE∥AB且DE＝AB
∴△DEO∽△ABO
∴
∴
同理，可证另外两条中线
∴三角形顶点到重心的距离等于该顶点对边上中线长的
（2）
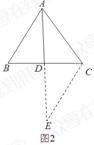
如图2，AD为△ABC的角平分线过点C作AB的平行线CE交AD的延长线于E
则∠BAD=∠E
∵AD为△ABC的角平分线
∴∠BAD=∠CAD
∴∠E=∠CAD
∴AC＝CE
∵CE∥AB
∴△BAD∽△CED
∴
∴