如图：△ABC中，D是AB上一点，AD=AC，BC边上的中线AE交CD于F。
求证：

答案

证明：（方法一）如图

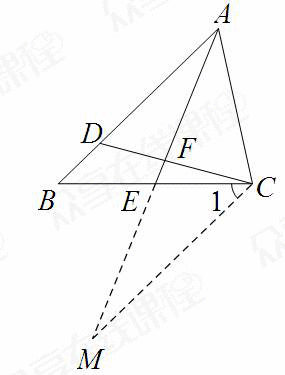
延长AE到M使得EM=AE，连接CM
∵BE=CE，∠AEB=∠MEC
∴ △BEA≌△CEM
∴CM=AB，∠1=∠B
∴AB∥CM
∴∠M=∠MAD，∠MCF=∠ADF
∴△MCF∽△ADF
∴
∵CM=AB，AD=AC
∴
（方法二）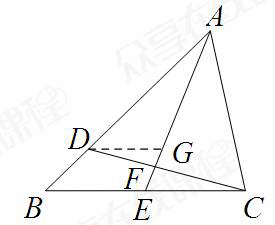
过D作DG∥BC交AE于G
则△ABE∽△ADG，△CEF∽△DGF
∴，
∵AD=AC，BE=CE
∴