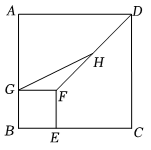
如图,正方形ABCD和正方形BEFG的边长分别为6和2,点E,G分别在边BC,AB上,点H为DF的中点,连接GH,则GH的长为____.
答案
知识点:略
延长GH交AD的延长线于N,如图:
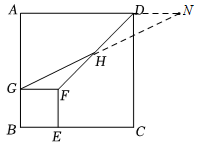
∵正方形ABCD和正方形AEFG的边长分别为6和2,
∴BE∥GF∥AD,GF=BG=2,AB=AD=6,
∴∠FGH=∠N,GA=4,
∵点H是DF的中点,
∴DH=FH,
在△FGH和△CNH中,
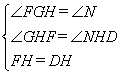
∴△FGH≌△DNH(AAS),
∴GH=HN,GF=DN=2,
∴AN=AD+DN=8,
在Rt△AGN中,∠A=90°,
由勾股定理得![]() ,
,
∴GH=![]() GN=
GN=![]() .
.
故答案为![]()
略





