如图①，E为矩形ABCD的边AD上一点，点P从点B出发折线B→E→D运动到点D停止，点Q从点B出发沿BC运动到C停止，它们的运动速度都是1cm/s，设运动时间为x（s），△BPQ的面积为y（cm²）．若y与x的对应关系如图②所示，则矩形ABCD的面积是(    )

• A.72 cm²
• B.84 cm²
• C.96 cm²
• D.56 cm²

答案

正确答案：A

知识点：一次函数的性质  

从函数的图象和运动的过程可以得出：DE=14-10=4（cm）
当点P运动到点E时，x=10s，y=30cm²，
过点E作EH⊥BC于H，

由三角形面积公式得：（cm²）
解得EH=AB=6cm，
∴AE=（cm）
由图2可知当x=14时，点P与点D重合，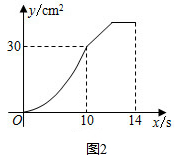

∴AD=AE+DE=8+4=12（cm），
∴矩形的面积为12×6=72（cm²）．
故选：A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>