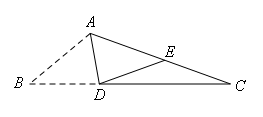
如图,将△ABD沿△ABC的角平分线AD翻折,点B恰好落在AC边上的点E处.已知∠C=20°,AB+BD=AC,那么∠B的度数为( )
- A.30°
- B.40°
- C.60°
- D.80°
答案
正确答案:B
由翻折可得:△ABD与△AED关于AD对称,
所以AB=AE,BD=DE,∠B=∠AED,∠ADB=∠ADE,
因为AB+BD=AC,AC=AE+CE=AB+CE,
所以BD=CE,
所以DE=CE,
所以∠C=∠EDC,
因为∠C=20°,
所以∠EDC=20°,
所以∠BDE=180°-∠EDC=160°,
所以∠ADB=∠ADE=![]() ∠BDE=80°,
∠BDE=80°,
所以∠ADC=∠ADE+∠EDC=100°,
所以∠DAC=180°-∠ADC-∠C=60°,
所以∠BAC=2∠DAC=120°,
所以∠B=180°-∠BAC-∠C=40°.
故选:B.
略





