等腰三角形一腰上的高与另一腰的夹角为54°，则该等腰三角形底角的度数为(    )

在等腰△ABC中，AB=AC，BD为腰AC上的高，∠ABD=54°，
当BD在△ABC内部时，如图1，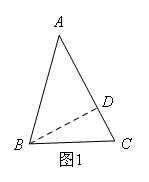

因为BD为高，
所以∠ADB=90°，
所以∠BAD=90°-54°=36°，
因为AB=AC，
所以∠ABC=∠ACB=(180°-36°)=72°；
当BD在△ABC外部时，如图2，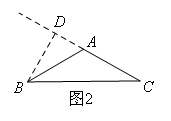

因为BD为高，
所以∠ADB=90°，
所以∠BAD=90°-54°=36°，
因为AB=AC，
所以∠ABC=∠ACB，
而∠BAD=∠ABC+∠ACB，
所以∠ACB=∠BAD=18°，
综上所述，这个等腰三角形底角的度数为72°或18°．
故选：D．

略