如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,则△AMN的周长为()
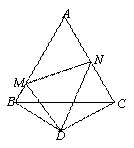
- A.1
- B.2
- C.3
- D.4
答案
正确答案:B
知识点:三角形全等的判定及性质
如图,在AC延长线上截取CE,使得CE=BM,连接DE,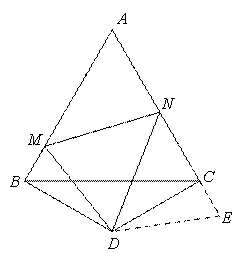
∵△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,
∴∠ABC=∠ACB=60°,∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴∠DCE=90°,
∵BD=CD,在△BDM和△CDE中,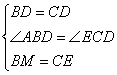
∴△BDM≌△CDE(SAS),
∴MD=ED,∠MDB=∠EDC,
∴∠MDE=120°-∠MDB+∠EDC=120°,
∴∠NDE=60°,
∵MD=ED,∠MDN=∠NDE=60°,DN=DN,
∴△MDN≌△EDN,
∴MN=NE,故△AMN的周长=AM+MN+AN=AM+AN+NE=AM+AE=AB+AC=2.
略








