为了鼓励城市周边农民种菜的积极性,某公司计划新建A、B两种温室80栋,将其售给农民种菜.该公司为建设温室所筹建资金不少于209.6万元,但不超过210.2万元,且所筹资金全部用于新建温室.两种温室的成本和出售价如下表:

(1)这两种温室有几种设计方案?
(2)根据市场调查,每栋A型温室的售价不会改变,每栋B型温室的售价可降低m万元(0<m<0.7),且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少.
答案
(1)设建A型温室x栋,则建B型温室建(80-x)栋.
根据题意,得209.6≤2.5x+2.8(80-x)≤210.2
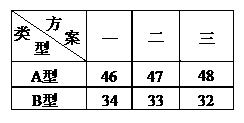
解得46≤x≤48.(x取整数)
故x=46,47,48,新建温室的方案如下:
(2)设建温室利润为y万元,
则y=(3.1-2.5)x+(3.5-2.8-m)(80-x)
即y=(m-0.1)x+56-80m
①当m=0.1时,无论x为何值,y恒为48万元
②当0.1<m<0.7时,y随x的增大而增大,即x=46时,y最小
③当0<m<0.1时,y随x的增大而减小,即x=48时,y最小
综上,当m=0.1时,三种方案所获利润一样
当0.1<m<0.7时,建A型温室46栋,B型温室34栋利润最小
当0<m<0.1时,建A型温室48栋,B型温室32栋利润最小
知识点:一次函数的应用
略
略








