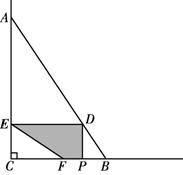
如图，∠C=90°，点A、B在∠C的两边上，CA=30，CB=20，连结AB.点P从点B出发，以每秒4个单位长度的速度沿BC方向运动，到点C停止.当点P与B、C两点不重合时，作PD⊥BC交AB于D，作DE⊥AC交AC于E.F为射线CB上一点，且∠CEF=∠ABC.设点P的运动时间为x（秒）.
（1）用含有x的代数式表示CF的长.
（2）求点F与点B重合时x的值.
（3）当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y（平方单位）.求y与x之间的函数关系式.
答案
（1）∵PD⊥BC，DE⊥AC，且∠C=90°，
∴四边形DECP为矩形，∴DE=PC，DP=EC，
又∵∠CEF=∠ABC，
∴△ABC∽△DBP∽△FEC，
∴
，
∵CA=30，CB=20，BP=4x，
∴
，
∴DP=EC=6x，CF=9x.
（2）当点F与点B重合时，FC=BC，
∴FC=BC，
∴9x=20，解得：x=
.
（3）由（2）得，当点F与点B重合时，x=
当点F与点P重合时，
CF+BP=BC，即9x+4x=20
解得x=
当0＜x≤
时，阴影部分为梯形
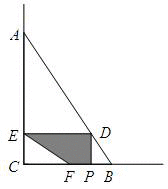
∵FP=BC-FC-PB=20-9x-4x=20-13x，
∵DE=PC=BC-PB=20-4x，
∴S=（DE+FP）•DP•0.5=（20-4x+20-13x）•6x×0.5=3x（40-17x）=120x-51x2；
当＜x≤时，阴影部分面积即为所求
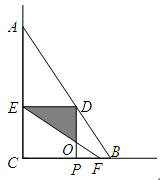
矩形DECP中DP∥EC，
∴∠DOE=∠FEC，
∴Rt△DOE∽Rt△CEF，
∴
，
∴
，
∴DO=
（20-4x），
∴S=
DO•DE=×（20-4x）（20-4x）=
.
知识点：勾股定理 矩形的判定与性质 相似三角形的判定和性质
略
略
WORD格式（
