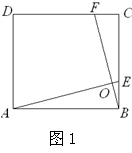
(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.

(2)如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH,交于点O,∠FOH=90°,EF=4,求GH的长。
答案
(1)证明:如图1,∵四边形ABCD为正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠EAB+∠AEB=90°.
∵∠EOB=∠AOF=90°,
∴∠FBC+∠AEB=90°,
∴∠EAB=∠FBC,
∴△ABE≌△BCF,
∴BE=CF.
(2)解:如图:过点A作AM//GH交BC于M,过点B作BN//EF交CD于N,AM与BN交于点O′,
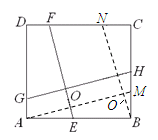
则四边形AMHG和四边形BNFE均为平行四边形,
∴EF=BN,GH=AM,
∵∠FOH=90°,AM//GH,EF//BN,
∴∠NO′A=90°,
故由(1)得, △ABM≌△BCN,
∴AM=BN,
∴GH=EF=4.
知识点:全等三角形的性质 全等三角形的判定 正方形的性质 开放探究型问题
略
略









