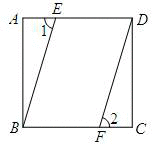
如图,正方形ABCD中,E与F分别是AD、BC上一点.在①AE=CF,②BE∥DF,③∠1=∠2中,请选择其中一个条件,证明BE=DF.(1)你选择的条件是 (只需填写序号),请证明;(2)在BE=DF的前提下,当E点位于AD什么位置时,EF∥CD?请说明理由.
答案
(1)解法一:①.
证明:∵四边形ABCD是正方形,
∴AB=CD,∠A=∠C=∠90°.
又∵AE=CF,
∴△AEB≌△CFD,
∴BE=DF.
解法二:②.
证明:∵四边形ABCD是正方形,
∴AD∥BC.
又∵BE∥DF,
∴四边形EBFD是平行四边形,
∴BE=DF.
解法三:③.
证明:∵四边形ABCD是正方形,
∴AB=CD,∠A=∠C=∠90°
又∵∠1=∠2,
∴△AEB≌△CFD.
∴BE=DF.
(2)当E位于AD中点时,EF∥CD,
理由:∵BE=DF,AB=CD,
∴Rt△AEB≌Rt△CFD.
∴AE=CF,
又∵AE=DE,
∴DE=CF,
又∵DE∥CF,
∴四边形EDCF是平行四边形,
∴EF∥CD.
知识点:全等三角形的判定与性质 平行四边形的判定 正方形的性质
略
略








