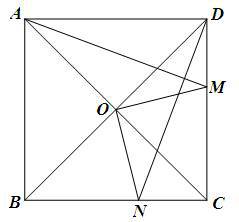
如图，在正方形ABCD的边CD上任取一点M，过点D作DN⊥AM交BC于点N，设正方形对角线交点为O，试确定OM与ON之间的关系，并说明理由．
答案
解：OM与ON之间的关系是OM=ON；OM⊥ON，理由如下：
∵四边形ABCD是正方形，
∴DC=DA，∠ADM=∠DCN=90°，
又∵DN⊥AM交BC于N，
∴∠MAD+∠ADN=90°，
而∠NDC+∠ADN=90°，
∴∠MAD=∠NDC，
在△ADM和△DCN中
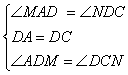
∴△ADM≌△DCN（ASA）
∴DM=CN
再根据四边形ABCD是正方形可以得到
OD=OC，∠ODM=∠OCN=45°，
在△ODM和△OCN中
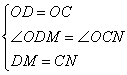
∴△ODM≌△OCN（SAS）
∴OM=ON，∠DOM=∠CON，
而∠COM+∠DOM=90°，
∴∠COM+∠CON=90°．
∴∠MON=90°．
∴OM与ON之间的关系是OM=ON；OM⊥ON．
知识点：三角形全等性质与判定
略
略
WORD格式（
