如图,P为正方形ABCD的对称中心,A(0,3),B(1,0),直线OP交AB于N,DC于M,点R从O出发沿OM方向运动.
求:(1)C的坐标为 ;
(2)当△ANO与△DMR相似时,求点R的坐标.

答案
解答思路:
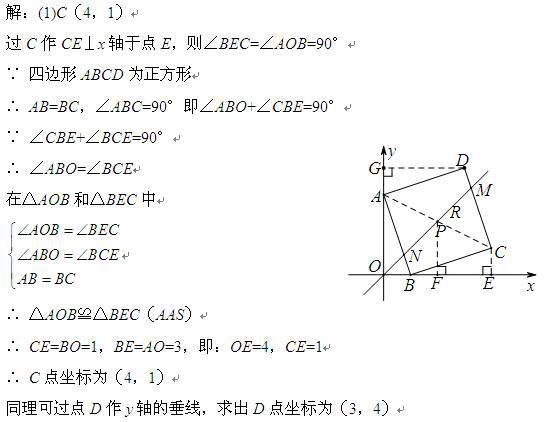
(2)过点P作PF⊥x轴于点F,则PF∥CE
∵P为正方形ABCD的对称中心
∴AP=CP
∴PF为梯形AOEC的中位线
∴![]() ,OF=EF=2
,OF=EF=2
∴点P的坐标为(2,2)
∴直线OP所在直线解析式为:y=x
∵AB∥CD
∴∠ANO=∠DMR
当△ANO与△DMR相似时,分为两种情况
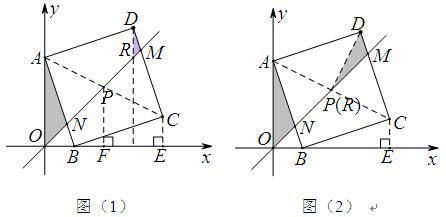
①△ANO∽△DMR时,如图(1)∠ANO=∠DMR,∠NAO=∠MDR
过D作DR∥OA交OM于点R,则R点即为所求
∵点D坐标为(3,4),DR∥y轴,点R在直线y=x上
∴点R坐标为(3,3)
②△ANO∽△RMD时,如图(2)∠ANO=∠DMR,∠AON=∠RDM=45°
∴点R与点P重合,为正方形ABCD的对称中心
∴点R坐标为(2,2)
知识点:函数背景下的相似问题
略
略








