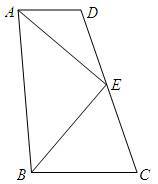
如图，AD∥BC，AE、BE分别平分∠DAB、∠CBA，CD经过点E，求证：AB=AD+BC
答案
证明：如图，在AB上截取AF，使得AF=AD，连接EF（如图）
∵AD∥CB
∴∠CBA+∠BAD=180°
∵BE平分∠CBA，AE平分∠BAD
∴∠ABE=∠EBC=
∠ABC，∠DAE=∠EAF=∠DAF
∴∠EBA+∠BAE=90°
∴∠BEA=180°-90°=90°
即BE⊥AE
在△ADE和△AFE中
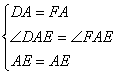
∴△ADE≌△AFE（SAS）
∴∠1=∠2，
又∵∠2+∠3=90°，∠1+∠4=90°
∴∠3=∠4
在△BCE和△BFE中
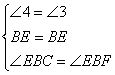
∴△BCE≌△BFE（ASA）
∴BC=BF
∴AB=AF+BF=AD+BC
知识点：三角形全等之截长补短
略
略
WORD格式（
