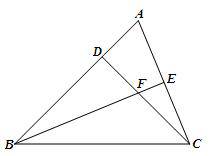
已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F。
（1）求证：BF=AC；
（2）求证：CE=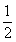BF．

答案

证明：（1）∵∠ABC=45°，CD⊥AB，
∴∠ABC=∠DCB=45°，BD=CD∠A＋∠ACD=90°
∵BE⊥AC
∴∠A＋∠ABE=90°
∴∠ACD=∠ABE
在△BDF和△CDA中，

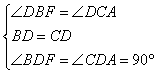
∴△BDF≌△CDA（ASA）
∴BF=AC
（2）∵BE平分∠ABC
∴∠ABE=∠CBE
在△ABE和△CBE中，

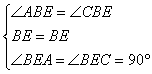
∴△ABE≌△CBE（ASA）
∴AE=CE
∴CE=AC=BF

知识点：三角形全等性质与判定  

略

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>