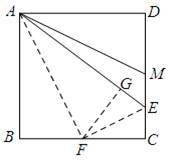
如图，已知正方形ABCD中，M为CD的中点，E为MC上一点，且∠BAE=2∠DAM．
求证：AE=BC+CE．

答案

证明：如图，过A作AF平分∠BAE交BC于F，过F做FG⊥AE于G，连接EF，则BF=FG，∠BAF=∠GAF=∠DAM

在Rt△ABF与Rt△AGF中

∴Rt△ABF≌Rt△AGF（HL）
∴AB=AG，BF=GF
∵四边形ABCD为正方形
∴AB=AD=BC，∠B=∠D=90°
在△ABF与△ADM中

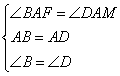
∴△ABF≌△ADM（ASA）
∴BF=DM
∵M为DC中点
∴DM=CM=CD
∴BF=CF=CB
∴CF=FG
在Rt△GFE与Rt△CFE中

∴Rt△GFE≌Rt△CFE（HL）
∴GE=CE
∴AE=AG+GE=BC+CE