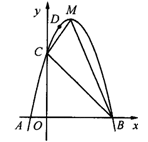
如图所示，二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A，B两点，其中A点坐标为（－1，0），点C（0，5），D（1，8）在抛物线上，M为抛物线的顶点．
（1）求抛物线的解析式；
（2）求△MCB的面积．

（1）∵A（-1，0），C（0，5），D（1，8）三点在抛物线y=ax²+bx+c上，
则有-a+b+c=0，c=5，a+b+c=8
得a=-1，b=4，c=5
所以抛物线解析式为y=-x²+4x+5．
（2）∵y=-x²+4x+5
=-（x-5）（x+1）
=-（x-2）²+9
∴M（2，5），B（5，0）
即BC= = =，
由B、C两点坐标得直线BC的解析式为：x+y-5=0，
则点M到直线AB的距离为d= = ，
则S_△MCB= ×BC×d=15．

对二次函数图象的相关知识与函数系数的联系掌握不牢