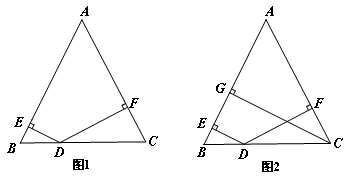
已知：如图，D是等腰△ABC底边BC上一点，它到两腰AB、AC的距离分别为DE、DF．
（1）如图1，当D点在什么位置时，DE=DF？并加以证明．
（2）如图2，探索DE、DF与等腰△ABC腰上的高的关系．

（1）当D为BC的中点时，DE=DF．
理由：∵AD为等腰三角形底边上的中线，
∴AD平分∠BAC，
又∵DE⊥AB，DF⊥AC，
∴DE=DF．
（2）CG=DE+DF．
理由如下：连接AD，
由S_△ABC=S_△ABD+S_△ACD= AB·CG=AB·DE+AB·DF，
∵AB=AC，
∴CG=DE+DF．

略