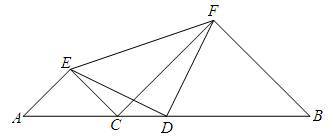
如图，D为线段AB的中点，在AB上取异于D的点C，分别以AC、BC为斜边在AB同侧作等腰直角三角形ACE与BCF，连接DE、DF、EF。
求证：△DEF为等腰直角三角形．

答案

证明：延长ED到点G，使得DG=DE，连接BG，FG

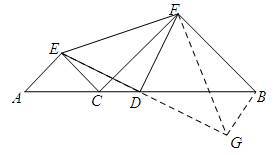
∵D为线段AB的中点
∴AD=BD
在△EDA和△GDB中，

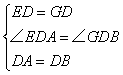
∴△EDA≌△GDB（SAS）
∴EA=GB，∠A=∠GBD
∵△ACE与△BCF都是等腰直角三角形
∴AE=CE=BG，CF=FB，∠A=∠ECA=∠FCB=∠FBC=45°∴∠ECF=90°，∠FBG=∠FBD+∠GBD=90°
在△ECF和△GBF中，

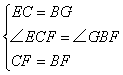
∴△ECF≌△GBF（SAS）
∴EF=GF，∠EFC=∠GFB
∵∠CFB=∠CFG+∠GFB=90°
∴∠EFG=∠EFC+∠CFG=90°
在△EFD和△GFD中，

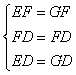
∴△EFD≌△GFD（SSS）
∴∠EDF=∠GDF=90°，∠EFD=∠GFD=45°，ED=DF
∴△DEF为等腰直角三角形