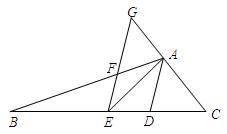
如图，在三角形ABC中，AB>AC，E为BC的中点，AD为∠BAC的平分线，过E做AD的平行线，交AB于F，交CA得延长线于G。
求证BF=CG．
答案
证明：延长GE到点H，使得EH=GE，连接BH
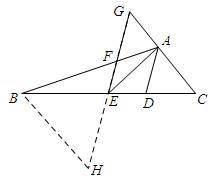
∵E为BC的中点
∴BE=CE
在△BEH和△CEG中，
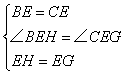
∴△BEH≌△CEG（SAS）
∴∠H=∠G
∵AD为∠BAC的平分线
∴∠BAD=∠CAD
∵AD∥GE
∴∠BAD=∠BFH，∠G=∠CAD
∴∠BFG=∠G=∠H
∴BF=CG
知识点：三角形全等之倍长中线
略
略
WORD格式（
