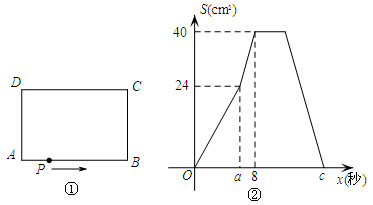
如图①，在矩形ABCD中，AB=10cm，BC=8cm，点P从A出发，沿A→B→C→D路线运动，到D停止，点P的速度为每秒1cm，a秒时点P改变速度，变为每秒bcm，图②是点P出发x秒后△APD的面积S（cm2）与x（秒）的关系图象，
（1）参照图②，求a、b及图②中的c值；
（2）设点P离开点A的路程为y（cm），请写出动点P改变速度后y与出发后的运动时间x（秒）的关系式，并求出点P到达DC中点时x的值．
（3）当点P出发多少秒后，△APD的面积是矩形ABCD面积的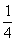
．
．
答案
解：（1）由图得知：S△APD=
AD·AP=×8×1×a=24
∴a=6
b=
=
=2
c=8+
=17
(2)y=6+2(x-6)=2x-6(6≤x≤17)
P到达DC中点时，
y=10+8+10×=23
即23=2x-6
x=
(3)当P在AB中点和CD中点时，S△APD=
S矩形ABCD
当P在AB中点时，P出发5秒；
当P在CD中点时，代入（2）中y=2x-6
即23=2x-6
x=
∴P出发5秒和秒时，S△APD=S矩形ABCD。
知识点：常量与变量之间的关系
略
略
WORD格式（
